Du problème de transport à la distance de Gromov-Wassertein

Bon ça fait quelques jours que j’ai un rythme de vie assez minable, je me dis que j’irai lire puis dormir aux alentours de 23h et au final je me perds sur internet jusqu’à 2 voire 3h du matin, moment auquel je m’endors naturellement d’épuisement. Le matin je me réveille aux alentours de 7h30 puis je rentre dans un cycle où je m’endors, chaque fois le temps d’un rêve, me réveille puis recommence le processus jusqu’à ce que je sois vraiment obligé de me lever pour me rendre à un rendez-vous ou pour me mettre à travailler si je souhaite faire quelque chose de ma matinée.

Ce soir, au lieu de glander sur internet, je préfère partager un petit peu ce sur quoi je galère en ce moment, dans le cadre du projet de recherche que je mène cet été. Ce dernier porte sur l’étude de propriétés de graphs dans le cadre notamment des Graph Neural Network et un point central de cet étude et l’utilisation de la distance de Gromov-Wassertein et de ses variantes. En bref ce post est une sorte de checkpoint sur ce qu’est Gromov-Wasserstein essayant de donner du contexte à ces outils. Le but n’est pas de produire un texte très rigoureux, plusieurs hypothèses (que j’avoue ne pas toujours très bien comprendre) seront omises.

Alors voilà, le point de départ et le suivant : c’est l’été, vous êtes à la plage et vous vous retrouvez avec un certain nombre de tas de sable, agencés aléatoirement, et un certain nombre de trous de profondeur égale à la quantité totale de sable présent dans les tas. Vous voulez remplir les trous avec le sable présent dans les tas (et uniquement dans les tas) en minimisant la dépense d’énergie nécessaire pour effectuer la tâche.

C’est ce qu’on appellera problème du transport, la théorie mathématique fondée sur ce problème est appelée théorie du Transport Optimal.

Mesure

En reprenant l’analogie des tas de sable, il nous faut trouver une manière de représenter ces distribution, de sable. Ceci se fera à partir de la notion de mesure que l’on peut voir comme une distribution de poids réparti sur l’espace considéré.

Dans le cas d’une distribution discrète (c’est à dire prenant un nombre fini, raisonnable de valeurs) on considèrera des mesures de la forme \(\alpha \in \mathcal{M}(X)\) \(\alpha = \sum_{i=1}^{n} a_i \delta{x_i}\) → où $\delta(x_i)$ est défini une masse de dirac, c’est à dire $\delta{x_i} = 1 $ si $x = x_i$ et 0 sinon, pour $ \forall x \in X \subset \mathbb{R}^n$

Dans le cas plus général notre tas de sable sera représenté comme une densité $\rho_\alpha(x)$ définie par rapport à la mesure de Lebesgue et vérifiant la relation

\[\forall f \in C^0(X), \quad \int_{X} h(x) \, d\alpha(x) = \int_{X} h(x) \, \rho_\alpha(x) \, dx\]

A noter que la mesure ne se traduit qu’à travers l’intégrale d’une fonction par cette même mesure, sur un sous-ensemble de l’espace de définition.

Tout comme une densité de probabilité est une mesure, elle n’est sondée qu’à travers une intégrale recouvrant un sous ensemble de l’espace des issues pour y assigner une valeur que l’on interprète comme probabilité.

Formulation de Monge

Une formulation très simple du problème est d’imaginer un certain nombre n de tas de sable chacun ayant une quantité $a_i$, $i \in {0, \dots, n}$ de sable et un même nombre m = n de trous pouvant contenir chacun une quantité $b_j$, avec $j \in {0, \dots, m}$ de sable. Et pour chaque couple de trous et de tas sable, on associe un coefficient $c(i,j)$ qui représente le coût de transportation du tas de sable i jusqu’au trou j. Le but est de trouver la meilleure manière de boucher tous les trous and déplaçant chaque tas de sable vers un des trous i.e le meilleur plan de transport de la distribution des tas de sables vers la distribution des trous (vus comme des mesures)

En réécrivant les coefficient de coût dans une matrice $(C_{i,j})_{i,j} = c(i,j)$, trouver une solution à ce problème est équivalent à trouver une permutation $\sigma$ des n tas de sables :

\[\min_{\sigma \in \text{Perm}(n)} \sum_{i=1}^{n} C_{i, \sigma(i)}\]

Ce problème est communément appelé problème d’affectation.

En généralisant le problème d’affectation à des mesures discrètes quelquconques alpha et beta telles que :

\(\alpha \in \mathcal{M}(X)\) \(\beta \in \mathcal{M}(Y)\) \(\alpha = \sum_{i=1}^{n} a_i \delta{x_i}\) \(\beta = \sum_{i=1}^{n} b_i \delta{y_i}\)

On tombe sur ce qu’on appelle le problème de Monge pour mesures discrètes et on peut formaliser le problème en

\[\min_{T} \sum_i c(x_i, T(x_i)) \quad \text{tel que} \quad T_{\#} \alpha = \beta\]

Où $T : {x_1, \dots, x_n} \rightarrow {y_1, \dots, y_m} \quad$ est tel que \(\quad \forall j \in \{1, \dots, m\}, \quad b_j = \sum_{\substack{i \\ T(x_i) = y_j}} a_i\)

C’est à dire que T determine une manière de transporter chaque tas de sable vers un unique trou tout en conservant la masse initiale.

Alors que $T$ donne un plan de déplacement d’une masse ponctuelle de sable vers un trou, $T_{\sharp}$ est l’opérateur associé à $T$ qui, à une mesure quelconque, associe sa mesure image par la fonction $T$. ($T_{\sharp} \alpha = \beta$ signifie donc que déplacer $\alpha$ en utilisant $T$ donne la mesure $\beta$.)

De manière plus générale on écrira le problème de Monge pour deux mesures arbitraires :

\[\min_{T} \int_{X} c(x, T(x)) \, d\alpha(x) \quad \text{tel que} \quad T_{\#} \alpha = \beta\]

Avec cette formulation, on peut se heurter à un problème :

T, tel qu’il est formulé ne permet que de déplacer “toute la masse présente à un point” vers un autre point. Or il n’existe pas toujours de solution selon la configuration initiale du problème qui puisse nous fournir une manière de transporter les mesures de cette manière tout en conservant la masse totale.(par exemple les cas m>n)

Formulation de Kantorovich

Une solution à notre problème précédement évoquée est de s’autoriser à envoyer la quantité de masse présente à un point de l’espace, vers plusieurs points différents. C’est l’idée derrière la méthode de Kantorovich. Cette fois ci, nous n’utiliserons plus un objet qui pour chaque point de l’espace de départ spécifie un seul point de l’espace d’arrivée mais plutôt ce qu’on appelle un “coupling” qui encode une manière de déplacer la masse de chaque point de l’espace de départ vers un ou plusieurs points de l’espace d’arrivée.

Dans le cas discret on peut simplement encoder ce mapping dans une matrice P dans laquelle chaque entrée Pij spécifie la quantité de masse envoyée du point i au point j. Par construction il nous faut $P1_m = a $ et $P^\top1_m = b $. Où a respectivement b sont le distributions discrètes de départ resp. d’arrivée, econdées dans un vecteur de taille n resp. m.

Si on encode le cout de chaque déplacement dans une matrice C, le problème de transport sous le prisme de Kantorovich s’écrit :

\[\min_{P} \sum_{i,j} C_{i,j} P_{i,j} = \min_{P} \langle C, P \rangle\]

Où P est une matrice telle que $P_{i,j}$ définit la masse du point $x_i$ à envoyer au point $y_j$. Par conservation de la masse, P doit donc être de telle sorte que $\sum_{j}P_{i,j} = a_i$ et $\sum_{i}P_{i,j} = b_j$. Le produit scalaire correspond à celui de Frobenius (extension du produit scalaire euclidien à l’espace des matrices).

Formellement le problème de kantorovich pour des mesures discrètes s’écrit :

\[\min_{P \in U(\alpha, \beta)} \langle C, P \rangle = \min_{P \in U(\alpha, \beta)} \operatorname{Tr}(C^\top P)\] \[U(\alpha, \beta) = \left\{ P \in \mathbb{R}_+^{n \times m} \;\middle|\; \sum_{j=1}^{m} P_{i,j} = a_i, \; \sum_{i=1}^{n} P_{i,j} = b_j \right\}\]

Étendu à des mesures arbitraires, on définit $\pi \in \mathcal{M}_+(X \times Y)$ comme une distribution jointe entre la mesure de départ et la mesure d’arrivée, c’est-à-dire que $\pi(A \times Y) = \alpha(A)$ et $\pi(X \times B) = \beta(B)$. Cette mesure encode nos plans de transport.

On définit l’ensemble des plans admissibles, c’est-à-dire les $\pi$ qui respectent la conservation de la masse, par :

\[U(\alpha, \beta) := \left\{ \pi \in \mathcal{M}_+^1(X \times Y) \;\middle|\; (P_X)_{\sharp} \pi = \alpha \;\text{et}\; (P_Y)_{\sharp} \pi = \beta \right\}\]

où

\[(P_Y)_{\sharp} \pi(B) := \pi(X \times B), \quad (P_X)_{\sharp} \pi(A) := \pi(A \times Y)\]

désignent les mesures images de $\pi$ par les projections sur $Y$ et $X$, respectivement.

La solution du problème de Kantorovich s’écrit alors :

\[\mathcal{L}_c(\alpha, \beta) := \min_{\pi \in U(\alpha, \beta)} \int_{X \times Y} c(x, y)\, d\pi(x, y)\]

Distance de Wasserstein

La théorie du transport optimal permet de poser un cadre quant à la recherche de la transformation d’une mesure à une autre qui minimise un certain coût. On peu alors naturellement se demander si on peut quantifier à quel point une certaine mesure est différente d’une autre en utilisant les outils que l’on vient d’évoquer. Il est clair que cette quantification sera dépendante du coût associé au transport. C’est ceci que réalise la distance de Wasserstein, pour deux distribution.

En supposant que $c(x, y) = d(x, y)^p$,

On défini : \(W_p(\alpha, \beta) := \left( \min_{\pi \in U(\alpha, \beta)} \int_{X \times Y} d(x, y)^p \, d\pi(x, y) \right)^{1/p}\)

qui constitue une distance s’appuyant sur le coût de transport entre deux mesures définies sur le même espace métrique, que l’on appelle p-distance de Wasserstein.

Distance de Gromov-Wassertstein

Dans tout ce qui précède, on supposait enfaite implicitement que nos mesures vivaient dans le même espace métrique (par l’utilisation des égalitées en terme d’intégration et utilisation du même coût représenté par une distance de l’espace, dans la formulation de la métrique de Wasserstein)

Dans beaucoup de cas, il est très utile de pouvoir comparer deux “objets” qui ne vivent pas dans le même espace. C’est dans ce cadre qu’intervient la distance de Gromov-Wasserstein que l’on définit, pour deux espaces métriques munis d’une mesure $ (X, d_X, \alpha_X) $ et $ (Y, d_Y, \alpha_Y) $ comme :

\[\mathcal{GW}\left( (\alpha_X, d_X), (\alpha_Y, d_Y) \right) := \left( \min_{\pi \in U(\alpha_X, \alpha_Y)} \iint_{(X \times Y)^2} \left| d_X(x, x') - d_Y(y, y') \right|^2 \, d\pi(x, y) \, d\pi(x', y')\right)^{1/2}\]

Intuitivement, Gromov revient à chercher dans chaque espace respectif à quel point il est coûteux de déplacer la mesure d’un espace de la même manière que la mesure de l’autre espace, ce qui revient à chercher des similarité dans la structure de chaque mesure dans leur espace respectif.

Miscellaneous

Les distances de Wasserstein, de Gromov et les autres dérivée de la théorie du transport optimal ont plein d’applications notamment en traitement d’image et Machine Learning. J’ai d’ailleurs trouvé quelques images marrantes qui suivent ce principe :

Aussi j’ai hésité à mettre cette image là dans l’intro afin d’illustrer une mesure discrète faite de masses de Dirac, genre qu’est ce qui leur a pris mdrrr ?

Il y a quasiment un an jour pour jour, je faisais un stage dans le labo DOLA et ce jour là il n’y avait que moi et Alex (un post-doc) présent au labo. A la pause midi, il m’expliquait en quoi consistait ses recherches, je me rappellle n’y avoir quasiment rien compris, il travaillait sur des problèmes de transport optimal. Je suis content d’y voir légèrement plus clair maintenant. Si on reprenait la discussion aujourd’hui j’aurai au moins une idée à peine plus élaborée de ce que représente une mesure haha.

Le contenu de ce post est grandement inspiré du livre “Computational Optimal Transport” de G.Peyré et M.Cuturi

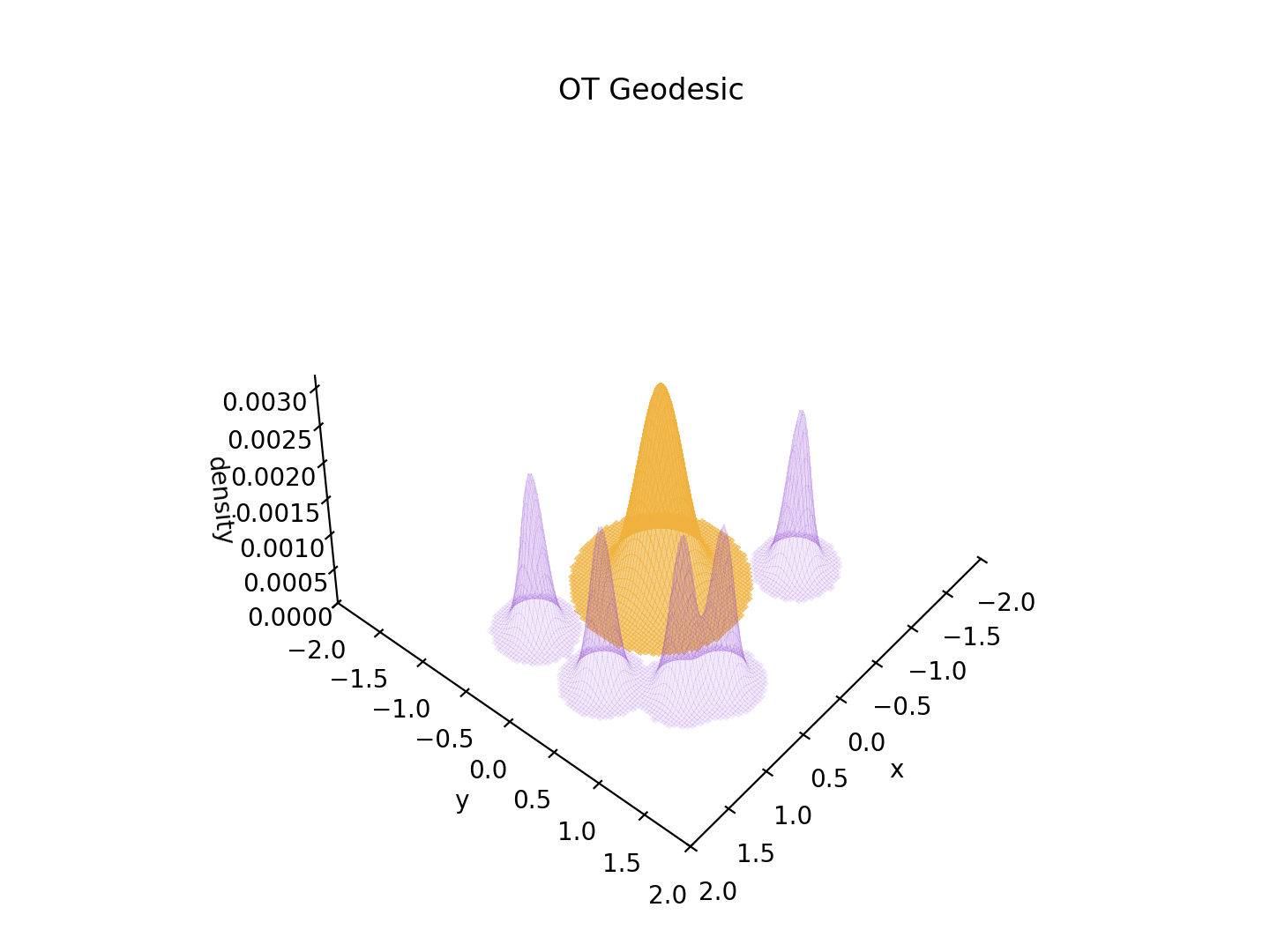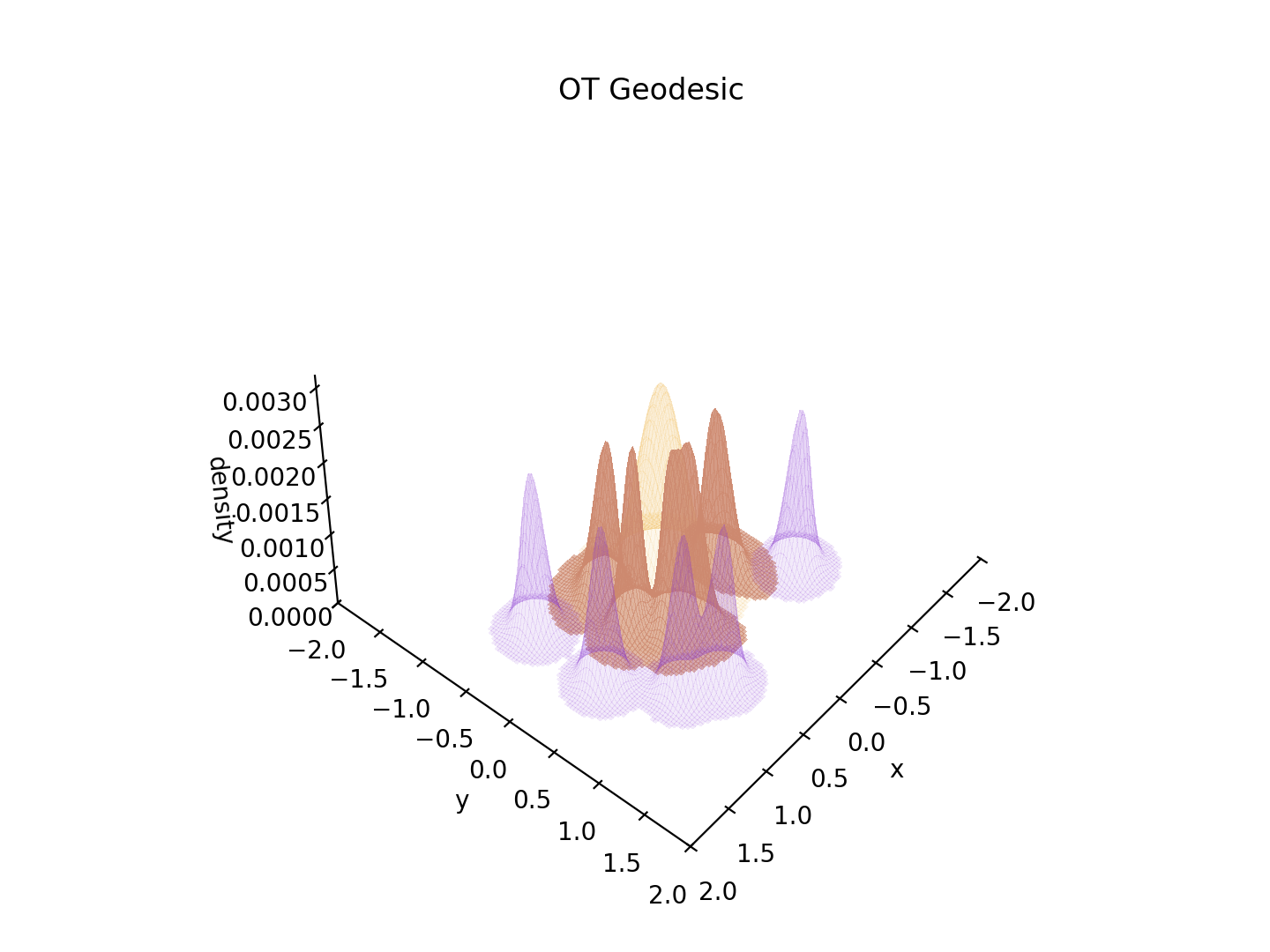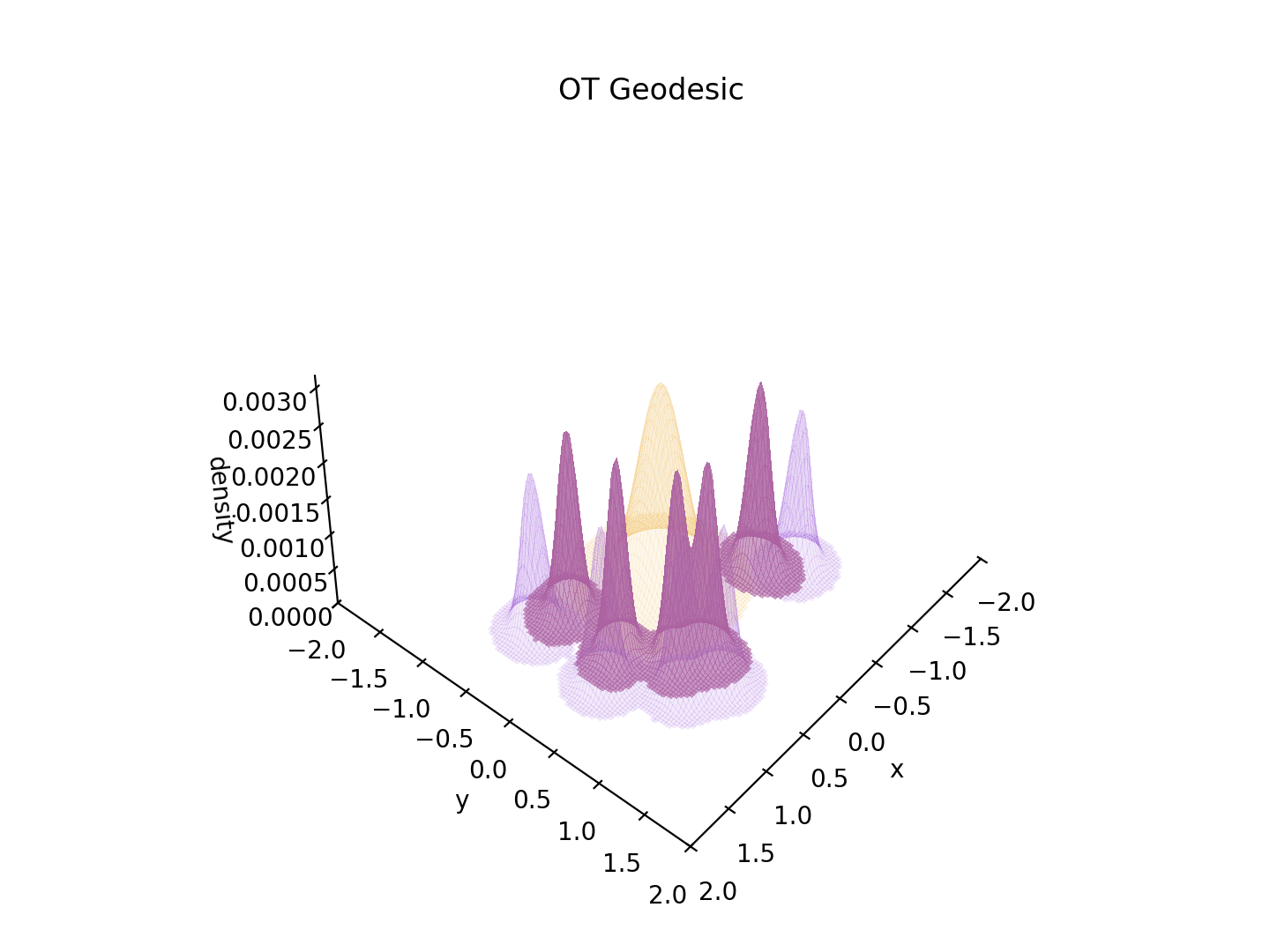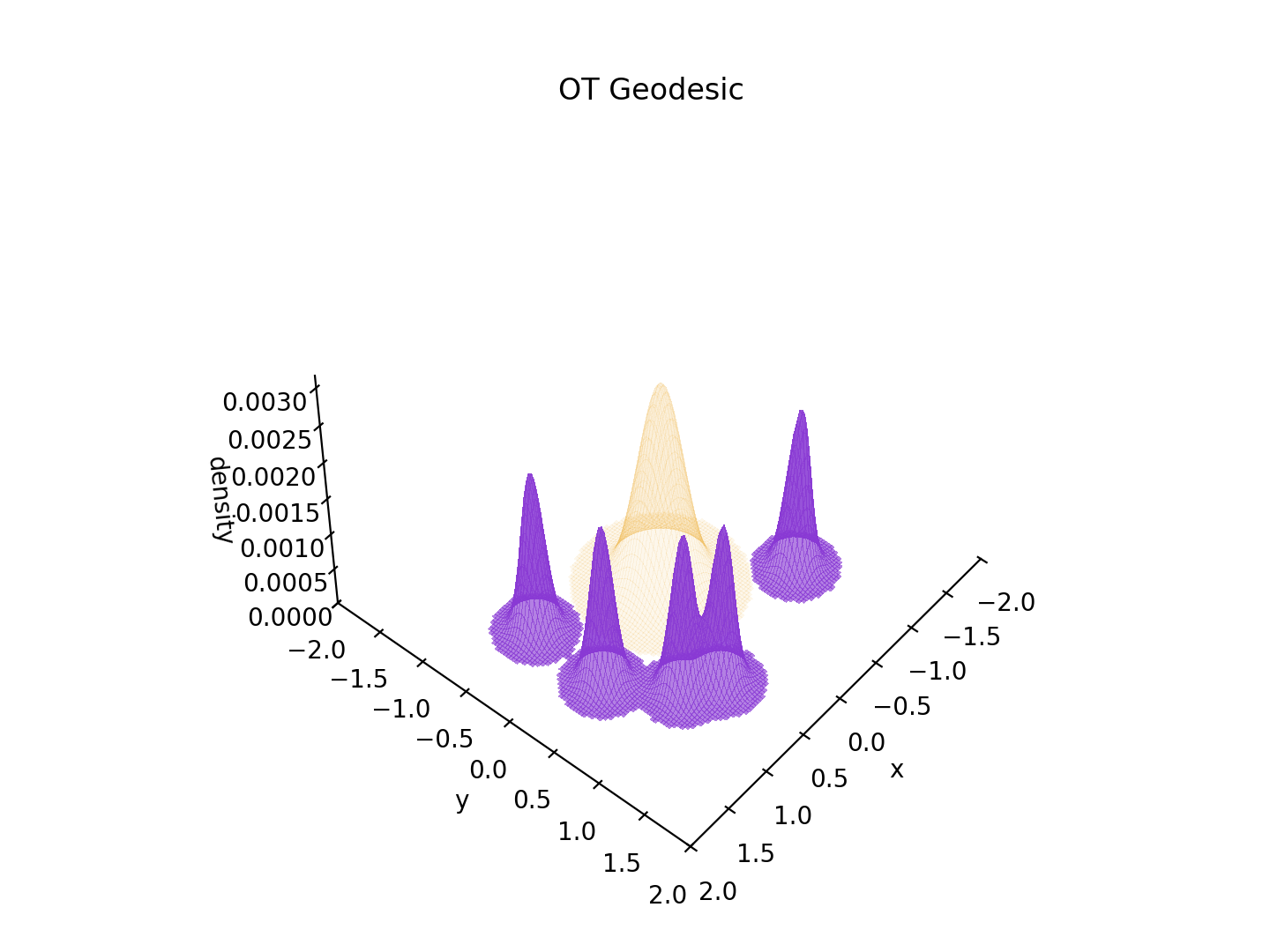
Edit 19/08/2025 : Je m’amusais à faire des animations de transformations optimales (géodésiques) d’une mesure à une autre. Voilà pour illustrer un “transport optimal” entre un “gros tas de sable” et plusieurs “petits autres tas de sable (ou trous mais là en l’occurence ils sont dans le mauvais sens)”

_