Je suis actuellement de passage chez mes parents, après avoir fini mes examens, le temps de respirer un coup avant de reprendre mes différentes activités d’été. Et à mesure que je revois mes amis d’ici je sens une transition dans mon état émotionnel, mes pensée, mes réflexion : le passage d’un état post-examen à (enfin) le début de l’été.

Alors voilà ce post servira à ajouter du contenu à ce blog qui depuis quelques semaines est bien peu dynamique, il ne cherche pas à être spécialement travaillé ou intéressant, si ce n’est afin de briser cette possible pression (bon le mot est fort) associée à la volonté de faire le “bon post”, comme on a pu l’évoquer en discutant avec Max tout à l’heure.

J’aime l’idée de pouvoir imprimer cette “sensation” post-exam avant qu’elle ne se dissipe complètement, et ce, dans l’espoir de réussir à reproduire ou du moins à renvoyer, à mon futur moi (ou bien à toi), cet ensemble de sensations qui régissent mon état. Idéalement j’aimerai que le contenu de ce post puisse renvoyer à un souvenir non seulement accompagné d’une image mais aussi d’un son, d’une odeur et d’un goût. Je ne sais pas à quel point il m’est possible de partager mon état actuel, ni à quel point un quelconque lecteur pourra se mettre à ma place et s’imaginer quelque chose de proche. Finalement je me contenterai d’écrire ce qui me passe par la tête, en espérant que cela suscite une quelconque émotion au lecteur.

Une forte partie des images qui m’ont traversé l’esprit en ce moment sont dûs à certains concepts que j’ai découverts (ou re-découvert) en binge-apprenant mes différents cours, 2 à 3 jours précédant l’examen concerné.

Je pense que le truc qui m’est le plus revenu sont les fractales de Newton:

Cette figure presque psychédélique est donc une fractale qu’on peut obtenir en coloriant chaque point de l’ensemble de départ avec une couleur associée à la racine vers laquelle on converge, lorsqu’on applique l’algorithme de Newton sur une fonction de ℂ dans ℂ, avec une certaine régularité (qui admet plusieurs racines, holomorphe mais pas trop plate sinon l’algorithme pose problème). Simplement, l’algorithme de Newton permet de trouver les zéros d’une fonction en procédant de manière itérative : on commence par choisir un point de départ, puis, à chaque étape, on approxime la fonction au point courant par sa tangente (un développement au premier ordre). On utilise ensuite cette approximation pour avancer vers le point où la tangente s’annule, (Dans R ça serait l’endroit où elle coupe l’axe des abscisses). On répète ce processus jusqu’à se rapprocher suffisamment d’un zéro de la fonction de départ.

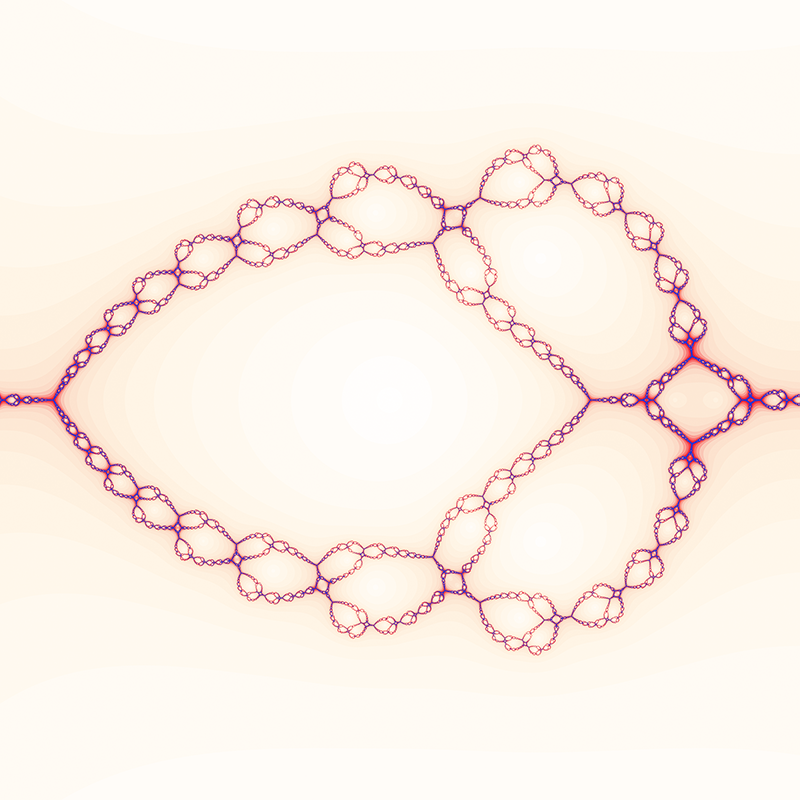
Au-delà du fait que ce soit très joli, ça m’évoque surtout que même un algorithme qui, à priori, semble assez clair et prévisible peut avoir un comportement complètement non trivial et produire une structure qui semble aléatoire, mais qui est pourtant bien ordonnée, car se répétant à l’infini.

Les images sont tirées des sites https://ryhl.io/blog/newton-intro/ et https://paulbourke.net/fractals/newtonraphson/

J’ai développé une sorte d’obsession pour cette vidéo :

Je ne sais pas ce qui capture le plus mon intérêt : ces deux lycéens et leur manière un peu geek et bizarre de bouger (surtout en ce qui concerne Ryan) qui m’évoque quelque chose d’assez familier, un peu comme si je les connaissais; ou la musique faisant partie de ce club prestigieux dans lequel toutes les mélodies sont des exactes copies de “Dota” par Basshunter (Je ne sais même pas si c’est bien celle-ci l’originale mais c’est la première que j’ai découvert). Alors voilà quelques “chansons” qui ont exactement ou presque cette même mélodie :

https://www.youtube.com/watch?v=flL_2awF-QI

https://www.youtube.com/watch?v=qTsaS1Tm-Ic

https://www.youtube.com/watch?v=P3CxhBIrBho

https://www.youtube.com/watch?v=1IIPioL6rqw

https://www.youtube.com/watch?v=P1L9q1TLIko

C’est quand même je pense la seule topline qui à ma connaissance a été autant reprise et essorée, et pourtant je ne m’en lasse pas. Pour en revenir à la vidéo ça doit faire 2-3 semaines que j’y retourne régulièrement, je trouve que tout y est génial, sans vraiment comprendre pourquoi (à part la fin qui me met particulièrement mal à l’aise).